I do not suppose that Newton would in any case have produced much more original work after his illness; but his appointment in 1696 as warden, and his promotion in 1699 to the mastership of the Mint, at a salary of £ 1500 a year, brought his scientific investigations to an end, though it was only after this that many of his previous investigations were published in the form of books. In 1696 he moved to London, in 1701 he resigned the Lucasian chair, and in 1703 he was elected president of the Royal Society.

In 1704 Newton published his Optics, which contains the results of the papers already mentioned. To the first edition of this book were appended two minor works which have no special connection with optics; one being on cubic curves, the other on the quadrature of curves and on fluxions. Both of them were manuscripts with which his friends and pupils were familiar, but they were here published urbi et orbi for the first time.

The first of these appendices is entitled Enumeratio Linearum Tertii Ordinis; the object seems to be to illustrate the use of analytical geometry, and as the application to conics was well known, Newton selected the theory of cubics.

He begins with some general theorems, and classifies curves according as their equations are algebraical or transcendental; the former being cut by a straight line in a number of points (real or imaginary) equal to the degree of the curve, the latter being cut by a straight line in an infinite number of points. Newton then shews that many of the most important properties of conics have their analogues in the theory of cubics, and he discusses the theory of asymptotes and curvilinear diameters.

After these general theorems, he commences his detailed examination of cubics by pointing out that a cubic must have at least one real point at infinity. If the asymptote or tangent at this point be a finite distance, it may be taken for the axis of y. This asymptote will cut the curve in three points altogether, of which at least two are at infinity. If the third point be at a finite distance, then (by one of his general theorems on asymptotes) the equation can be written in the form

where the axes of x and y are the asymptotes of the hyperbola which is the locus of the middle points of all chords drawn parallel to the axis of y; while, if the third point in which this asymptote cuts the curve be also at infinity, the equation can be written in the form

Next he takes the case where the tangent at the real point at infinity is not at a finite distance. A line parallel to that direction in which the curve goes to infinity may be taken as the axis of y. Any such line will cut the curve in three points altogether, of which one is by hypothesis at infinity, and one is necessarily at a finite distance. He then shews that if the remaining point in which this line cuts the curve be at a finite distance, the equation can be written in the form

while if it be at an infinite distance, the equation can be written in the form

Any cubic is therefore reducible to one of four characteristic forms. Each of these forms is then discussed in detail, and the possibility of the existence of double points, isolated ovals, etc., is worked out. The final result is that in all there are seventy-eight possible forms which a cubic may take. Of these Newton enumerated one seventy-two; four of the remainder were mentioned by Stirling in 1717, one by Nicole in 1731, and one by Nicholas Bernoulli about the same time.

 

In the course of the work Newton states the remarkable theorem that, just as the shadow of a circle (cast by a luminous point on a plane) gives rise to all the conics, so the shadows of the curves represented by the equation

give rise to all the cubics. This remained an unsolved puzzle until 1731, when Nicole and Clairaut gave demonstrations of it; a better proof is that given by Murdoch in 1740, which depends on the classification of these curves into five species according as to whether their points of intersection with the axis of x are real and unequal, real and two of them are equal (two cases), real and all equal, or two imaginary and one real.

 

In this tract Newton also discusses double points in the plane and at infinity, the description of curves satisfying given conditions, and the graphical solution of problems by the use of curves.

The second appendix to the Optics is entitled De Quadratura Curvarum. Most of it had been communicated to Barrow in 1668 or 1669, and probably was familiar to Newton's pupils and friends from that time onwards. It consists of two parts.

The bulk of the first part is a statement of Newton's method of effecting the quadrature and rectification of curves by means of infinite series; it is noticeable as containing the earliest use in print of literal indices, and also the first printed statement of the binomial theorem, but these novelties are introduced only incidentally. The main object is to give rules for developing a function of x in a series in ascending powers of x, so as to enable mathematicians to effect the quadrature of any curve in which the ordinate y can be expressed as an explicit algebraical function of the abscissa x. Wallis had shewn how this quadrature could be found when y was given as a sum of a number of multiples of powers of x, and Newton's rules of expansion here established rendered possible the similar quadrature of any curve whose ordinate can be expressed as the sum of an infinite number of such terms. In this way he effects the quadrature of the curves

,

,

,

,

but naturally the results are expressed as infinite series. He then proceeds to curves whose ordinate is given as an implicit function of the abscissa; and he gives a method by which y can be expressed as an infinite series in ascending powers of x, but the application of the rule to any curve demands in general such complicated numerical calculations as to render it of little value. He concludes this part by shewing that the rectification of a curve can be effected in a somewhat similar way. His process is equivalent to finding the integral with regard to x of 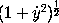  in the form of an infinite series. I should add that Newton indicates the importance of determining whether the series are convergent - an observation far in advance of his time - but he knew of no general test for the purpose; and in fact it was not until Gauss and Cauchy took up the question that the necessity of such limitations was commonly recognized.

 

The part of the appendix which I have just described is practically the same as Newton's manuscript De Analysi per Equationes Numero Terminorum Infinitas, which wa subsequently printed in 1711. It is said that this was originally intended to form an appendix to Kinckhuysen's Algebra, which, as I have already said, he at one time intended to edit. The substance of it was communicated to Barrow, and by him to Collins, in letters of July 31 and August 12, 1669; and a summary of it was included in the letter of October 24, 1676, sent to Leibnitz.

It should be read in connection with Newton's Methodus Differentialis, also published in 1711. Some additional theorems are there given, and he discusses his method of interpolation, which had been briefly described in the letter of October 24, 1676. The principle is this. If y = 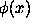  be a function of x, and if, when x is successively put equal to 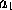, ,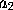..., the values of y be known and be 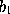, ,..., then a parabola whose equation is y = p + qx + rx² + ... 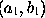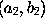can be drawn through the points , ,..., and the ordinate of this parabola may be taken as an approximation to the ordinate of the curve. The degree of the parabola will of course be one less than the number of given points. Newton points out that in this way the areas of any curves can be approximately determined.

The second part of this appendix to the Optics contains a description of Newton's method of fluxions. This is best considered in connection with Newton's manuscript on the same subject which was published by John Colson in 1736, and of which it is a summary.

The invention of the infinitesimal calculus was one of the great intellectual achievements of the seventeenth century. This method of analysis, expressed in the notation of fluxions and fluents, was used by Newton in or before 1666, but no account of it was published until 1693, though its general outline was known to his friends and pupils long anterior to that year, and no complete exposition of his methods was given before 1736.

The idea of a fluxion or differential coefficient, as treated at this time, is simple. When two quantities - e.g. the radius of a sphere and its volume - are so related that a change in one causes a change in the other, the one is said to be a function of the other. The ratio of the rates at which they change is termed the differential coefficient or fluxion of the one with regard to the other, and the process by which this ratio is determined is known as differentiation. Knowing the differential coefficient and one set of corresponding values of the two quantities, it is possible by summation to determine the relation between them, as Cavalieri and others had shewn; but often the process is difficult, if, however, we can reverse the process of differentiation we can obtain this result directly. This process of reversal is termed integration. It was at once seen that problems connected with the quadrature of curves, and the determination of volumes (which were soluble by summation, as had been shewn by the employment of indivisibles), were reducible to integration. In mechanics also, by integration, velocities could be deduced from known accelerations, and distances traversed from known velocities. In short, wherever things change according to known laws, here was a possible method of finding the relation between them. It is true that, when we try to express observed phenomena in the language of the calculus, we usually obtain an equation involving the variables, and their differential coefficients - and possibly the solution may be beyond our powers. Even so, the method is often fruitful, and its use marked a real advance in thought and power.

I proceed to describe somewhat fully Newton's methods as described by Colson. Newton assumed that all geometrical magnitudes might be conceived as generated by continuous motion; thus a line may be considered as generated by the motion of a point, a surface by that of a line, a solid by that of a surface, a plane angle by the rotation of a line, and so on. The quantity thus generated was defined by him as the fluent or flowing quantity. The velocity of the moving magnitude was defined as the fluxion of the fluent. This seems to be the earliest definite recognition of the idea of a continuous function, though it had been foreshadowed in some of Napier's papers.

Newton's treatment of the subject is as follows. There are two kinds of problems. The object of the first is to find the fluxion of a given quantity, or more generally ``the relation of the fluents being given, to find the relation of their fluxions.'' This is equivalent to differentiation. The object of the second or inverse method of fluxions is from the fluxion or some relations involving it to determine the fluent, or more generally ``an equation being proposed exhibiting the relation of the fluxions of quantities, to find the relations of those quantities, or fluents, to one another.'' This is equivalent either to integration which Newton termed the method of quadrature, or to the solution of a differential equation which was called by Newton the inverse method of tangents. The methods for solving these problems are discussed at considerable length.

Newton then went on to apply these results to questions connected with the maxima and minima of quantities, the method of drawing tangents to curves, and the curvature of curves (namely, the determination of the centre of curvature, the radius of curvature, and the rate at which the radius of curvature increases). He next considered the quadrature of curves and the rectification of curves. In finding the maximum and minimum of functions of one variable we regard the change of sign of the difference between two consecutive values of the function as the true criterion; but his argument is that when a quantity increasing has attained its maximum it can have no further increment, or when decreasing it has attained its minimum it can have no further decrement; consequently the fluxion must be equal to nothing.

It has been remarked that neither Newton nor Leibnitz produced a calculus, that is, a classified collection of rules; and that the problems they discussed were treated from first principles. That, no doubt, is the usual sequence in the history of such discoveries, though the fact is frequently forgotten by subsequent writers. In this case I think the statement, so far as Newton's treatment of the differential or fluxional part of the calculus is concerned, is incorrect, as the foregoing account sufficiently shews.

If a flowing quantity or fluent were represented by x, Newton denoted its fluxion by 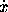, the fluxion of  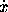 or second fluxion of x by 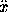, and so on. Similarly the fluent of x was denoted by 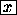, or sometimes by x' or [x]. The infinitely small part by which a fluent such as x increased in a small interval of time measured by o was called the moment of the fluent; and its value was shewn to be 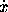o. Newton adds the important remark that thus we may in any problem neglect the terms multiplied by the second and higher powers of o, and we may always find an equation between the co-ordinates x, y of a point on a curve and their fluxions 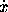, 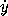. It is an application of this principle which constitutes one of the chief values of the calculus; for if we desire to find the effect produced by several causes on a system, then, if we can find the effect produced by each cause when acting alone in a very small time, the total effect produced in that time will be equal to the sum of the separate effects. I should here note the fact that Vince and other English writers in the eighteenth century used  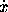 to denote the increment of x and not the velocity with which it increased; that is  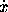 in their writings stands for what Newton would have expressed by 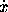o   and what Leibnitz would have written as dx.

I need not discuss in detail the manner in which Newton treated the problems above mentioned. I will only add that, in spite of the form of his definition, the introduction into geometry of the idea of time was evaded by supposing that some quantity ex. gr. the abscissa of a point on a curve) increased equably; and the required results then depend on the rate at which other quantities (ex. gr. the ordinate or radius of curvature) increase relatively to the one so chosen. The fluent so chosen is what we now call the independent variable; its fluxion was termed the ``principal fluxion''; and, of course, if it were denoted by x, then 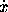  was constant, and consequently  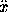 = 0.

There is no question that Newton used a method of fluxions in 1666, and it is practically certain that accounts of it were communicated in manuscript to friends and pupils from and after 1669. The manuscript, from which most of the above summary has been taken, is believed to have been written between 1671 and 1677, and to have been in circulation at Cambridge from that time onwards, though it is probable that parts were rewritten from time to time. It was unfortunate that it was not published at once. Strangers at a distance naturally judged of the method by the letter to Wallis in 1692, or by the Tractatus de Quadratura Curvarum, and were not aware that it had been so completely developed at an earlier date. This was the cause of numerous misunderstandings. At the same time it must be added that all mathematical analysis was leading up to the ideas and methods of the infinitesimal calculus. Foreshadowings of the principles and even of the language of that calculus can be found in the writings of Napier, Kepler, Cavalieri, Pascal, Fermat, Wallis, and Barrow. It was Newton's good luck to come at a time when everything was ripe for the discovery, and his ability enabled him to construct almost at once a complete calculus.

The infinitesimal calculus can also be expressed in the notation of the differential calculus: a notation which was invented by Leibnitz probably in 1675, certainly by 1677, and was published in 1684, some nine years before the earliest printed account of Newton's method of fluxions. But the question whether the general idea of the calculus expressed in that notation was obtained by Leibnitz from Newton, or whether it was discovered independently, gave rise to a long and bitter controversy. The leading facts are given in the next chapter.

The remaining events of Newton's life require little or no comment. In 1705 he was knighted. From this time onwards he devoted much of his leisure to theology, and wrote at great length on prophecies and predictions, subjects which had always been of interest to him. His Universal Arithmetic was published by Whiston in 1707, and his Analysis by Infinite Series in 1711; but Newton had nothing to do with the preparation of either of these for the press. His evidence before the House of Commons in 1714 on the determination of longitude at sea marks an important epoch in the history of navigation.

The dispute with Leibnitz as to whether he had derived the ideas of the differential calculus from Newton or invented it independently originated about 1708, and occupied much of Newton's time, especially between the years 1709 and 1716.

In 1709 Newton was persuaded to allow Cotes to prepare the long-talked-of second edition of the Principia; it was issued in March 1713. A third edition was published in 1726 under the direction of Henry Pemberton. In 1725 Newton's health began to fail. He died on March 20, 1727, and eight days later was buried in Westminster Abbey.

His chief works, taking them in their order of publication, are the Principia, published in 1687; the Optics (with appendices on cubic curves, the quadrature and rectification of curves by the use of infinite series, and the method of fluxions), published in 1704; the Universal Arithmetic, published in 1707; the Analysis per Series, Fluxiones, etc., and the Methodus Differentialis, published in 1711; the Lectiones Opticae, published in 1729; the Method of Fluxions, etc. (that is Newton's manuscript on fluxions), translated by J. Colson and published in 1736; and the Geometrica Analytica, printed in 1779 in the first volume of Horsley's edition of Newton's works.

In appearance Newton was short, and towards the close of his life rather stout, but well set, with a square lower jaw, brown eyes, a broad forehead, and rather sharp features. His hair turned grey before he was thirty, and remained thick and white as silver till his death.

As to his manners, he dressed slovenly, was rather languid, and was often so absorbed in his own thoughts as to be anything but a lively companion. Many anecdotes of his extreme absence of mind when engaged in any investigation have been preserved. Thus once when riding home from Grantham he dismounted to lead his horse up a steep hill; when he turned at the to remount, he found that he had the bridle in his hand, while his horse had slipped it and gone away. Again, on the few occasions when he sacrificed his time to entertain his friends, if he left them to get more wine or for any similar reason, he would as often as not be found after the lapse of some time working out a problem, oblivious alike of his expectant guests and of his errand. He took no exercise, indulged in no amusements, and worked incessantly, often spending eighteen or nineteen hours out of the twenty-four in writing.

In character he was religious and conscientious, with an exceptionally high standard of morality, having, as Bishop Burnet said, ``the whitest soul'' he ever knew. Newton was always perfectly straightforward and honest; but in his controversies with Leibnitz, Hooke and others, though scrupulously just, he was not generous; and it would seem that he frequently took offence at a chance expression when none was intended. He modestly attributed his discoveries largely to the admirable work done by his predecessors; and once explained that, if he had seen further than other men, it was only because he had stood on the shoulders of giants. He summed up his own estimate of his work in the sentence, ``I do not know what I may appear to the world; but to myself I seem to have been only like a boy, playing on the sea-shore, and diverting myself, in now and then finding a smoother pebble, or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.'' He was morbidly sensitive to being involved in any discussions. I believe that, with the exception of his papers on optics, every one of his works was published only under pressure from his friends and against his own wishes. There are several instances of his communicating papers and results on condition that his name should not be published: thus when in 1669 he had, at Collins's request, solved some problems on harmonic series and on annuities which had previously baffled investigation, he only gave permission that his results should be published ``so it be,'' as he says, ``without my name to it; for I see not what there is desirable in public esteem, were I able to acquire and maintain it: it would perhaps increase my acquaintance, the things which I chiefly study to decline.''

Perhaps the most wonderful single illustration of his powers was the composition in seven months of the first book of the Principia, and the expression of the numerous and complex results in classical geometrical form. As other illustrations of his ability I may mention his solutions of the problems of Pappus, of John Bernoulli's challenge, and of the question of orthogonal trajectories. The problem of Pappus, here alluded to, is to find the locus of a point such the rectangle under its distances from two given straight lines shall be in a given ratio to the rectangle under its distances from two other given straight lines. Many geometricians from the time of Apollonius had tried to find a geometrical solution and had failed, but what had proved insuperable to his predecessors seems to have presented little difficulty to Newton who gave an elegant demonstration that the locus was a conic. Geometry, said Lagrange when recommending the study of analysis to his pupils, is a strong bow, but it is one which only a Newton can fully utilize. As another example I may mention that in 1696 John Bernoulli challenged mathematicians (i) to determine the brachistochrone, and (ii) to find a curve such that if any line drawn from a fixed point O cut it in P and Q then 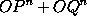  would be constant. Leibnitz solved the first of these questions after an interval of rather more than six months, and then suggested that they be sent as a challenge to Newton and others. Newton received the problems on Jan. 29, 1697, and the next day gave the complete solutions to both, at the same time generalising the second question. An almost exactly similar case occurred in 1716 when Newton was asked to find the orthogonal trajectory of a family of curves. In five hours Newton solved the problem in the form in which it was propounded to him, and laid down the principles for finding trajectories.

It is almost impossible to describe the effect of Newton's writings without being suspected of exaggeration. But, if the state of mathematical knowledge in 1669 or at the death of Pascal or Fermat be compared with what was known in 1700 it will be seen how immense was the advance. In fact we may say that it took mathematicians half a century or more before they were able to assimilate the work produced in those years.

In pure geometry Newton did not establish any new methods, but no modern writer has shewn the same power in using those of classical geometry. In algebra and the theory of equations he introduced the system of literal indices, established the binomial theorem, and created no inconsiderable part of the theory of equations: one rule which he enunciated in this subject remained till a few years ago an unsolved riddle which had overtaxed the resources of succeeding mathematicians. In analytical geometry, he introduced the modern classification of curves into algebraical and transcendental; and established many of the fundamental properties of asymptotes, multiple points, and isolated loops, illustrated by a discussion of cubic curves. The fluxional or infinitesimal calculus was invented by Newton in or before the year 1666, and circulated in manuscript amongst his friends in and after the year 1669, though no account of the method was printed till 1693. The fact that the results are nowadays expressed in a different notation has led to Newton's investigations on this subject being somewhat overlooked.

Newton, further, was the first to place dynamics on a satisfactory basis, and from dynamics he deduced the theory of statics: this was in the introduction to the Principia published in 1687. The theory of attractions, the application of the principles of mechanics to the solar system, the creation of physical astronomy, and the establishment of the law of universal gravitation are due to him, and were first published in the same work, but of the nature of gravity he confessed his ignorance, though he found inconceivable the idea of action at a distance. The particular questions connected with the motion of the earth and moon were worked out as fully as was then possible. The theory of hydrodynamics was created in the second book of the Principia, and he added considerably to the theory of hydrostatics which may be said to have been first discussed in modern times by Pascal. The theory of the propagation of waves, and in particular the application to determine the velocity of sound, is due to Newton and was published in 1687. In geometrical optics, he explained amongst other things the decomposition of light and the theory of the rainbow; he invented the reflecting telescope known by his name, and the sextant. In physical optics, he suggested and elaborated the emission theory of light.

The above list does not exhaust the subjects he investigated, but it will serve to illustrate how marked was his influence on the history of mathematics. On his writings and on their effects, it will be enough to quote the remarks of two or three of those who were subsequently concerned with the subject-matter of the Principia. Lagrange described the Principia as the greatest production of the human mind, and said he felt dazed at such an illustration of what man's intellect might be capable. In describing the effect of his own writings and those of Laplace it was a favourite remark of his that Newton was not only the greatest genius that had ever existed, but he was also the most fortunate, for as there is but one universe, it can happen but to one man in the world's history to be the interpreter of its laws. Laplace, who is in general very sparing of his praise, makes of Newton the one exception, and the words in which he enumerates the causes which ``will always assure to the Principia a pre-eminence above all the other productions of human genius'' have been often quoted. Not less remarkable is the homage rendered by Gauss; for other great mathematicians or philosophers he used the epithets magnus, or clarus, or clarissimus: for Newton alone he kept the prefix summus. Finally Biot, who had made a special study of Newton's works, sums up his remarks by saying, ``comme géomètre et comme expérimentateur Newton est sans égal; par la réunion de ces deux genres de génies à leur plus haut degré, il est sans exemple.''

---

This page is included in a collection of mathematical biographies taken from A Short Account of the History of Mathematics by W. W. Rouse Ball (4th Edition, 1908).