Bir Çiftci olan babası o doğmadan üç ay önce ölmüştü. Oniki yaşında Grantham'da king's School'a yazılan Newton bu okulu 1661'de bitirdi. Aynı yıl Cambridge Universite'sindeki Trinity Kolleje girdi. Nisan 1665 'te bu okuldan lisans derecesini aldı. Lisansüstü çalışmalarına başlıyacağı sırada ortalığı saran veba salgını yüzünden üniversite kapatıldı.

         Salgından korunma amacıyla annesinin çiftliğine sığınan Newton burada geçirdiği iki yıl boyunca en önemli buluşlarını gerçekleştirdi. 1667'de Trinity Kolleje öğretim üyesi olarak döndüğünde diferansiyel ve integral hesabın temellerini atmış,beyaz ışığın renkli bileşenlerine ayrıştırılabileceğini saptamış ve cisimlerin birbirlerini, uzaklıklarının karesi ile ters orantılı olarak çektikleri sonucuna ulaşmıştı.Çekingenliği yüzünden Newton her biri bilimde devrim yaratacak nitelikteki bu buluşların çoğunu uzun yıllar sonra (örneğin diferansiyel ve integral hesabı 38 yıl sonra) yayımlamıştır.Lisansüstü çalışmasını ertesi yıl tamamlayan Newton 1669'da henüz 27 yaşındayken Cambridge Universite'sinde matematik profesörlüğüne getirildi.1671'de ilk aynalı teleskopu gerçekleştirdi, ve ertesi yıl Royal Society   üyeliğine seçildi. Royal Society'ye sunduğu renk olgusuna ilişkin bidirisinin eleştirilere hedef olması , özellikle Robert Hooke tarafından şiddetle eleştirilmesi üzerine  Newton tümüyle içine kapanarak, bilim dünyasıyle ilişkisini kesti. 1675'de sunduğu gene optik konusundaki iki bildirisi yeni tartışmalara yol açtı. Hooke makalelerdeki bazı sonuçların kendi buluşu olduğunu ,Newton'un bunlara sahip çıktığını öne sürdü.Bütün bu tartışma ve eleştiriler sonucunda 1678'de  ruhsal bunalıma giren Newton ancak yakın dostu ünlü astronom matematikçi Edmond Halley'in çabalarıyla altı yıl sonra bilimsel çalışmalarına geri döndü.
       Cambridge Universite'sinde katolikliği yaygınlaştırma ve egemen kılma çabalarına karşı başlatılan direniş hareketine öncülük eden Newton, kral düşürüldükten sonra 1689'da üniversitenin parlamento daki temsilciliğine seçildi. 1693'de yeniden bir ruhsal bunalıma girdi ve yakın dostlarıyla, bu arada Samuel pepys ve John locke ile arası bozuldu.Iki yıl süren bir inziva döneminden sonra sağlığına yeniden kavuştuysada bundan sonraki yaşamında bilimsel çalışmaya eskisi gibi ilgi duymadı.Daha sonra 1699'da Fransız Bilimler Akademi'sinin yabancı üyeliğine 1703'de Royal Society'nin başkanlığına seçildi.
       Gelmiş geçmiş bilim adamlarının en büyüklerinden biri olarak kabul edilen Newton matematik ve fizikte çok önemli buluşlar gerçekleştirdi. Matematikte (a+b)ª  ifadesinin üstel seriye açınımını veren genel ikiterimli teoremini  buldu. Newton'un bilime en büyük katkısı mekanik alanındadır. Merkezkaç kuvvet yasası ile Kepler yasalarını birlikte ele alarak kütleçekim yasasını ortaya koydu. Newton hareket yasaları olarak bilinen eylemsizlik ilkesi, kuvvetin kütleyle ivmenin çarpımına eşit olduğunu ifade eden yasa ve etki ile tepkinin eşitliği fiziğin en önemli yasalarındandır.
     Yayımladığı kitaplardan bazıları Philosophiae naturalis principia mathematica, principia,opticks sayılabilir

Isaac Newton's life can be divided into three quite distinct periods. The first is his boyhood days from 1643 up to his appointment to a chair in 1669. The second period from 1669 to 1687 was the highly productive period in which he was Lucasian professor at Cambridge. The third period (nearly as long as the other two combined) saw Newton as a highly paid government official in London with little further interest in mathematical research.

Isaac Newton was born in the manor house of Woolsthorpe, near Grantham in Lincolnshire. Although by the calendar in use at the time of his birth he was born on Christmas Day 1642, we give the date of 4 January 1643 in this biography which is the "corrected" Gregorian calendar date bringing it into line with our present calendar. (The Gregorian calendar was not adopted in England until 1752.) Isaac Newton came from a family of farmers but never knew his father, also named Isaac Newton, who died in October 1642, three months before his son was born. Although Isaac's father owned property and animals which made him quite a wealthy man, he was completely uneducated and could not sign his own name.

You can see a picture of Woolsthorpe Manor as it is now.

Isaac's mother Hannah Ayscough remarried Barnabas Smith the minister of the church at North Witham, a nearby village, when Isaac was two years old. The young child was then left in the care of his grandmother Margery Ayscough at Woolsthorpe. Basically treated as an orphan, Isaac did not have a happy childhood. His grandfather James Ayscough was never mentioned by Isaac in later life and the fact that James left nothing to Isaac in his will, made when the boy was ten years old, suggests that there was no love lost between the two. There is no doubt that Isaac felt very bitter towards his mother and his step-father Barnabas Smith. When examining his sins at age nineteen, Isaac listed:-

Threatening my father and mother Smith to burn them and the house over them.

Upon the death of his stepfather in 1653, Newton lived in an extended family consisting of his mother, his grandmother, one half-brother, and two half-sisters. From shortly after this time Isaac began attending the Free Grammar School in Grantham. Although this was only five miles from his home, Isaac lodged with the Clark family at Grantham. However he seems to have shown little promise in academic work. His school reports described him as 'idle' and 'inattentive'. His mother, by now a lady of reasonable wealth and property, thought that her eldest son was the right person to manage her affairs and her estate. Isaac was taken away from school but soon showed that he had no talent, or interest, in managing an estate.

An uncle, William Ayscough, decided that Isaac should prepare for entering university and, having persuaded his mother that this was the right thing to do, Isaac was allowed to return to the Free Grammar School in Grantham in 1660 to complete his school education. This time he lodged with Stokes, who was the headmaster of the school, and it would appear that, despite suggestions that he had previously shown no academic promise, Isaac must have convinced some of those around him that he had academic promise. Some evidence points to Stokes also persuading Isaac's mother to let him enter university, so it is likely that Isaac had shown more promise in his first spell at the school than the school reports suggest. Another piece of evidence comes from Isaac's list of sins referred to above. He lists one of his sins as:-

... setting my heart on money, learning, and pleasure more than Thee ...

which tells us that Isaac must have had a passion for learning.

We know nothing about what Isaac learnt in preparation for university, but Stokes was an able man and almost certainly gave Isaac private coaching and a good grounding. There is no evidence that he learnt any mathematics, but we cannot rule out Stokes introducing him to Euclid's Elements which he was well capable of teaching (although there is evidence mentioned below that Newton did not read Euclid before 1663). Anecdotes abound about a mechanical ability which Isaac displayed at the school and stories are told of his skill in making models of machines, in particular of clocks and windmills. However, when biographers seek information about famous people there is always a tendency for people to report what they think is expected of them, and these anecdotes may simply be made up later by those who felt that the most famous scientist in the world ought to have had these skills at school.

Newton entered his uncle's old College, Trinity College Cambridge, on 5 June 1661. He was older than most of his fellow students but, despite the fact that his mother was financially well off, he entered as a sizar. A sizar at Cambridge was a student who received an allowance toward college expenses in exchange for acting as a servant to other students. There is certainly some ambiguity in his position as a sizar, for he seems to have associated with "better class" students rather than other sizars. Westfall (see [23] or [24]) has suggested that Newton may have had Humphrey Babington, a distant relative who was a Fellow of Trinity, as his patron. This reasonable explanation would fit well with what is known and mean that his mother did not subject him unnecessarily to hardship as some of his biographers claim.

Newton's aim at Cambridge was a law degree. Instruction at Cambridge was dominated by the philosophy of Aristotle but some freedom of study was allowed in the third year of the course. Newton studied the philosophy of Descartes, Gassendi, Hobbes, and in particular Boyle. The mechanics of the Copernican astronomy of Galileo attracted him and he also studied Kepler's Optics. He recorded his thoughts in a book which he entitled Quaestiones Quaedam Philosophicae (Certain Philosophical Questions). It is a fascinating account of how Newton's ideas were already forming around 1664. He headed the text with a Latin statement meaning "Plato is my friend, Aristotle is my friend, but my best friend is truth" showing himself a free thinker from an early stage.

How Newton was introduced to the most advanced mathematical texts of his day is slightly less clear. According to de Moivre, Newton's interest in mathematics began in the autumn of 1663 when he bought an astrology book at a fair in Cambridge and found that he could not understand the mathematics in it. Attempting to read a trigonometry book, he found that he lacked knowledge of geometry and so decided to read Barrow's edition of Euclid's Elements. The first few results were so easy that he almost gave up but he:-

... changed his mind when he read that parallelograms upon the same base and between the same parallels are equal.

Returning to the beginning, Newton read the whole book with a new respect. He then turned to Oughtred's Clavis Mathematica and Descartes' La Géométrie. The new algebra and analytical geometry of Viète was read by Newton from Frans van Schooten's edition of Viète's collected works published in 1646. Other major works of mathematics which he studied around this time was the newly published major work by van Schooten Geometria a Renato Des Cartes which appeared in two volumes in 1659-1661. The book contained important appendices by three of van Schooten's disciples, Jan de Witt, Johan Hudde, and Hendrick van Heuraet. Newton also studied Wallis's Algebra and it appears that his first original mathematical work came from his study of this text. He read Wallis's method for finding a square of equal area to a parabola and a hyperbola which used indivisibles. Newton made notes on Wallis's treatment of series but also devised his own proofs of the theorems writing:-

Thus Wallis doth it, but it may be done thus ...

It would be easy to think that Newton's talent began to emerge on the arrival of Barrow to the Lucasian chair at Cambridge in 1663 when he became a Fellow at Trinity College. Certainly the date matches the beginnings of Newton's deep mathematical studies. However, it would appear that the 1663 date is merely a coincidence and that it was only some years later that Barrow recognised the mathematical genius among his students.

Despite some evidence that his progress had not been particularly good, Newton was elected a scholar on 28 April 1664 and received his bachelor's degree in April 1665. It would appear that his scientific genius had still not emerged, but it did so suddenly when the plague closed the University in the summer of 1665 and he had to return to Lincolnshire. There, in a period of less than two years, while Newton was still under 25 years old, he began revolutionary advances in mathematics, optics, physics, and astronomy.

While Newton remained at home he laid the foundations for differential and integral calculus, several years before its independent discovery by Leibniz. The 'method of fluxions', as he termed it, was based on his crucial insight that the integration of a function is merely the inverse procedure to differentiating it. Taking differentiation as the basic operation, Newton produced simple analytical methods that unified many separate techniques previously developed to solve apparently unrelated problems such as finding areas, tangents, the lengths of curves and the maxima and minima of functions. Newton's De Methodis Serierum et Fluxionum was written in 1671 but Newton failed to get it published and it did not appear in print until John Colson produced an English translation in 1736.

When the University of Cambridge reopened after the plague in 1667, Newton put himself forward as a candidate for a fellowship. In October he was elected to a minor fellowship at Trinity College but, after being awarded his Master's Degree, he was elected to a major fellowship in July 1668 which allowed him to dine at the Fellows' Table. In July 1669 Barrow tried to ensure that Newton's mathematical achievements became known to the world. He sent Newton's text De Analysi to Collins in London writing:-

[Newton] brought me the other day some papers, wherein he set down methods of calculating the dimensions of magnitudes like that of Mr Mercator concerning the hyperbola, but very general; as also of resolving equations; which I suppose will please you; and I shall send you them by the next.

Collins corresponded with all the leading mathematicians of the day so Barrow's action should have led to quick recognition. Collins showed Brouncker, the President of the Royal Society, Newton's results (with the author's permission) but after this Newton requested that his manuscript be returned. Collins could not give a detailed account but de Sluze and Gregory learnt something of Newton's work through Collins. Barrow resigned the Lucasian chair in 1669 to devote himself to divinity, recommending that Newton (still only 27 years old) be appointed in his place. Shortly after this Newton visited London and twice met with Collins but, as he wrote to Gregory:-

... having no more acquaintance with him I did not think it becoming to urge him to communicate anything.

Newton's first work as Lucasian Professor was on optics and this was the topic of his first lecture course begun in January 1670. He had reached the conclusion during the two plague years that white light is not a simple entity. Every scientist since Aristotle had believed that white light was a basic single entity, but the chromatic aberration in a telescope lens convinced Newton otherwise. When he passed a thin beam of sunlight through a glass prism Newton noted the spectrum of colours that was formed.

He argued that white light is really a mixture of many different types of rays which are refracted at slightly different angles, and that each different type of ray produces a different spectral colour. Newton was led by this reasoning to the erroneous conclusion that telescopes using refracting lenses would always suffer chromatic aberration. He therefore proposed and constructed a reflecting telescope.

In 1672 Newton was elected a fellow of the Royal Society after donating a reflecting telescope. Also in 1672 Newton published his first scientific paper on light and colour in the Philosophical Transactions of the Royal Society. The paper was generally well received but Hooke and Huygens objected to Newton's attempt to prove, by experiment alone, that light consists of the motion of small particles rather than waves. The reception that his publication received did nothing to improve Newton's attitude to making his results known to the world. He was always pulled in two directions, there was something in his nature which wanted fame and recognition yet another side of him feared criticism and the easiest way to avoid being criticised was to publish nothing. Certainly one could say that his reaction to criticism was irrational, and certainly his aim to humiliate Hooke in public because of his opinions was abnormal. However, perhaps because of Newton's already high reputation, his corpuscular theory reigned until the wave theory was revived in the 19^th century.

Newton's relations with Hooke deteriorated further when, in 1675, Hooke claimed that Newton had stolen some of his optical results. Although the two men made their peace with an exchange of polite letters, Newton turned in on himself and away from the Royal Society which he associated with Hooke as one of its leaders. He delayed the publication of a full account of his optical researches until after the death of Hooke in 1703. Newton's Opticks appeared in 1704. It dealt with the theory of light and colour and with

1. investigations of the colours of thin sheets
   
2. 'Newton's rings' and
   
3. diffraction of light.
   

To explain some of his observations he had to use a wave theory of light in conjunction with his corpuscular theory.

Another argument, this time with the English Jesuits in Liège over his theory of colour, led to a violent exchange of letters, then in 1678 Newton appears to have suffered a nervous breakdown. His mother died in the following year and he withdrew further into his shell, mixing as little as possible with people for a number of years.

Newton's greatest achievement was his work in physics and celestial mechanics, which culminated in the theory of universal gravitation. By 1666 Newton had early versions of his three laws of motion. He had also discovered the law giving the centrifugal force on a body moving uniformly in a circular path. However he did not have a correct understanding of the mechanics of circular motion.

Newton's novel idea of 1666 was to imagine that the Earth's gravity influenced the Moon, counter- balancing its centrifugal force. From his law of centrifugal force and Kepler's third law of planetary motion, Newton deduced the inverse-square law.

In 1679 Newton corresponded with Hooke who had written to Newton claiming:-

... that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall ...

M Nauenberg writes an account of the next events:-

After his 1679 correspondence with Hooke, Newton, by his own account, found a proof that Kepler's areal law was a consequence of centripetal forces, and he also showed that if the orbital curve is an ellipse under the action of central forces then the radial dependence of the force is inverse square with the distance from the centre.

This discovery showed the physical significance of Kepler's second law.

In 1684 Halley, tired of Hooke's boasting [M Nauenberg]:-

... asked Newton what orbit a body followed under an inverse square force, and Newton replied immediately that it would be an ellipse. However in 'De Motu..' he only gave a proof of the converse theorem that if the orbit is an ellipse the force is inverse square. The proof that inverse square forces imply conic section orbits is sketched in Cor. 1 to Prop. 13 in Book 1 of the second and third editions of the 'Principia', but not in the first edition.

Halley persuaded Newton to write a full treatment of his new physics and its application to astronomy. Over a year later (1687) Newton published the Philosophiae naturalis principia mathematica or Principia as it is always known.

The Principia is recognised as the greatest scientific book ever written. Newton analysed the motion of bodies in resisting and non-resisting media under the action of centripetal forces. The results were applied to orbiting bodies, projectiles, pendulums, and free-fall near the Earth. He further demonstrated that the planets were attracted toward the Sun by a force varying as the inverse square of the distance and generalised that all heavenly bodies mutually attract one another.

Further generalisation led Newton to the law of universal gravitation:-

... all matter attracts all other matter with a force proportional to the product of their masses and inversely proportional to the square of the distance between them.

Newton explained a wide range of previously unrelated phenomena: the eccentric orbits of comets, the tides and their variations, the precession of the Earth's axis, and motion of the Moon as perturbed by the gravity of the Sun. This work made Newton an international leader in scientific research. The Continental scientists certainly did not accept the idea of action at a distance and continued to believe in Descartes' vortex theory where forces work through contact. However this did not stop the universal admiration for Newton's technical expertise.

James II became king of Great Britain on 6 February 1685. He had become a convert to the Roman Catholic church in 1669 but when he came to the throne he had strong support from Anglicans as well as Catholics. However rebellions arose, which James put down but he began to distrust Protestants and began to appoint Roman Catholic officers to the army. He then went further, appointing only Catholics as judges and officers of state. Whenever a position at Oxford or Cambridge became vacant, the king appointed a Roman Catholic to fill it. Newton was a staunch Protestant and strongly opposed to what he saw as an attack on the University of Cambridge.

When the King tried to insist that a Benedictine monk be given a degree without taking any examinations or swearing the required oaths, Newton wrote to the Vice-Chancellor:-

Be courageous and steady to the Laws and you cannot fail.

The Vice-Chancellor took Newton's advice and was dismissed from his post. However Newton continued to argue the case strongly preparing documents to be used by the University in its defence. However William of Orange had been invited by many leaders to bring an army to England to defeat James. William landed in November 1688 and James, finding that Protestants had left his army, fled to France. The University of Cambridge elected Newton, now famous for his strong defence of the university, as one of their two members to the Convention Parliament on 15 January 1689. This Parliament declared that James had abdicated and in February 1689 offered the crown to William and Mary. Newton was at the height of his standing - seen as a leader of the university and one of the most eminent mathematicians in the world. However, his election to Parliament may have been the event which let him see that there was a life in London which might appeal to him more than the academic world in Cambridge.

After suffering a second nervous breakdown in 1693, Newton retired from research. The reasons for this breakdown have been discussed by his biographers and many theories have been proposed: chemical poisoning as a result of his alchemy experiments; frustration with his researches; the ending of a personal friendship with Fatio de Duillier, a Swiss-born mathematician resident in London; and problems resulting from his religious beliefs. Newton himself blamed lack of sleep but this was almost certainly a symptom of the illness rather than the cause of it. There seems little reason to suppose that the illness was anything other than depression, a mental illness he must have suffered from throughout most of his life, perhaps made worse by some of the events we have just listed.

Newton decided to leave Cambridge to take up a government position in London becoming Warden of the Royal Mint in 1696 and Master in 1699. However, he did not resign his positions at Cambridge until 1701. As Master of the Mint, adding the income from his estates, we see that Newton became a very rich man. For many people a position such as Master of the Mint would have been treated as simply a reward for their scientific achievements. Newton did not treat it as such and he made a strong contribution to the work of the Mint. He led it through the difficult period of recoinage and he was particularly active in measures to prevent counterfeiting of the coinage.

In 1703 he was elected president of the Royal Society and was re-elected each year until his death. He was knighted in 1705 by Queen Anne, the first scientist to be so honoured for his work. However the last portion of his life was not an easy one, dominated in many ways with the controversy with Leibniz over which of them had invented the calculus.

Given the rage that Newton had shown throughout his life when criticised, it is not surprising that he flew into an irrational temper directed against Leibniz. We have given details of this controversy in Leibniz's biography and refer the reader to that article for details. Perhaps all that is worth relating here is how Newton used his position as President of the Royal Society. In this capacity he appointed an "impartial" committee to decide whether he or Leibniz was the inventor of the calculus. He wrote the official report of the committee (although of course it did not appear under his name) which was published by the Royal Society, and he then wrote a review (again anonymously) which appeared in the Philosophical Transactions of the Royal Society.

Newton's assistant Whiston had seen his rage at first hand. He wrote:-

Newton was of the most fearful, cautious and suspicious temper that I ever knew.

Isaac Newton

From Wikipedia, the free encyclopedia

 

Jump to: navigation, search

Sir Isaac Newton
Godfrey Kneller's 1689 portrait of Isaac Newton (aged 46)
Born	4 January 1643(1643-01-04) [OS: 25 December 1642][1] Woolsthorpe-by-Colsterworth Lincolnshire, England
Died	31 March 1727 (aged 84) [OS: 20 March 1726][1] Kensington, Middlesex, England
Residence	England
Citizenship	English
Nationality	English (British from 1707)
Fields	Physics, mathematics, astronomy, natural philosophy, alchemy, theology
Institutions	University of Cambridge Royal Society Royal Mint
Alma mater	Trinity College, Cambridge
Academic advisors	Isaac Barrow Benjamin Pulleyn[2][3]
Notable students	Roger Cotes William Whiston
Known for	Newtonian mechanics Universal gravitation Calculus Optics
Influences	Henry More
Influenced	Nicolas Fatio de Duillier John Keill
Religious stance	Monotheism; for details see article
Signature
Notes His mother was Hannah Ayscough. His half-niece was Catherine Barton.

Sir Isaac Newton, FRS (4 January 1643  – 31 March 1727 [OS: 25 December 1642 – 20 March 1726])^[1] was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian and one of the most influential men^[4] in human history. His Philosophiæ Naturalis Principia Mathematica, published in 1687, is considered to be the most influential book in the history of science. In this work, Newton described universal gravitation and the three laws of motion, laying the groundwork for classical mechanics, which dominated the scientific view of the physical Universe for the next three centuries and is the basis for modern engineering. Newton showed that the motions of objects on Earth and of celestial bodies are governed by the same set of natural laws by demonstrating the consistency between Kepler's laws of planetary motion and his theory of gravitation, thus removing the last doubts about heliocentrism and advancing the scientific revolution.

In mechanics, Newton enunciated the principles of conservation of momentum and angular momentum. In optics, he built the first "practical" reflecting telescope^[5] and developed a theory of colour based on the observation that a prism decomposes white light into a visible spectrum. He also formulated an empirical law of cooling and studied the speed of sound.

In mathematics, Newton shares the credit with Gottfried Leibniz for the development of the differential and integral calculus. He also demonstrated the generalised binomial theorem, developed the so-called "Newton's method" for approximating the zeroes of a function, and contributed to the study of power series.

Newton was also highly religious (though unorthodox), producing more work on Biblical hermeneutics than the natural science he is remembered for today.

Newton's stature among scientists remains at the very top rank, as demonstrated by a 2005 survey of scientists in Britain's Royal Society asking who had the greater effect on the history of science, Newton or Albert Einstein. Newton was deemed the more influential.^[6]

Contents [hide] 1 Biography 1.1 Early years 1.2 Middle years 1.2.1 Mathematics 1.2.2 Optics 1.2.3 Mechanics and gravitation 1.3 Later life 2 Religious views 2.1 Newton's effect on religious thought 2.2 Views of the end of the world 3 Newton and the counterfeiters 4 Enlightenment philosophers 5 Newton's laws of motion 6 Newton's apple 7 Writings by Newton 8 Fame 9 Newton in popular culture 10 Monuments and commemoration 11 See also 12 Footnotes and references 13 Resources 13.1 References 13.2 Further reading 13.3 Newton and religion 13.4 Primary sources 14 External links

Biography

Early years

Main article: Isaac Newton's early life and achievements

Isaac Newton was born on 4 January 1643 [OS: 25 December 1642]^[1] at Woolsthorpe Manor in Woolsthorpe-by-Colsterworth, a hamlet in the county of Lincolnshire. At the time of Newton's birth, England had not adopted the latest papal calendar and therefore his date of birth was recorded as Christmas Day, 25 December 1642. Newton was born three months after the death of his father. Born prematurely, he was a small child; his mother Hannah Ayscough reportedly said that he could have fit inside a quart mug. When Newton was three, his mother remarried and went to live with her new husband, the Reverend Barnabus Smith, leaving her son in the care of his maternal grandmother, Margery Ayscough. The young Isaac disliked his stepfather and held some enmity towards his mother for marrying him, as revealed by this entry in a list of sins committed up to the age of 19: Threatening my father and mother Smith to burn them and the house over them.^[7]

Newton in a 1702 portrait by Godfrey Kneller

Isaac Newton (Bolton, Sarah K. Famous Men of Science. NY: Thomas Y. Crowell & Co., 1889)

A replica of Newton's 6-inch (150 mm) reflecting telescope of 1672 for the Royal Society.

According to E.T. Bell and H. Eves:

Newton began his schooling in the village schools and was later sent to The King's School, Grantham, where he became the top student in the school. At King's, he lodged with the local apothecary, William Clarke and eventually became engaged to the apothecary's stepdaughter, Anne Storer, before he went off to the University of Cambridge at the age of 19. As Newton became engrossed in his studies, the romance cooled and Miss Storer married someone else. It is said he kept a warm memory of this love, but Newton had no other recorded "sweet-hearts" and never married.^[8]

There are rumours that he remained a confirmed celibate.^[9] However, Bell and Eves' sources for this claim, William Stukeley and Mrs. Vincent (the former Miss Storer – actually named Katherine, not Anne), merely say that Newton entertained "a passion" for Storer while he lodged at the Clarke house.

From the age of about twelve until he was seventeen, Newton was educated at The King's School, Grantham (where his signature can still be seen upon a library window sill). He was removed from school, and by October 1659, he was to be found at Woolsthorpe-by-Colsterworth, where his mother, widowed by now for a second time, attempted to make a farmer of him. He hated farming. Henry Stokes, master at the King's School, persuaded his mother to send him back to school so that he might complete his education. This he did at the age of eighteen, achieving an admirable final report.

In June 1661, he was admitted to Trinity College, Cambridge. According to John Stillwell, he entered Trinity as a sizar.^[10] At that time, the college's teachings were based on those of Aristotle, but Newton preferred to read the more advanced ideas of modern philosophers such as Descartes and astronomers such as Copernicus, Galileo, and Kepler. In 1665, he discovered the generalised binomial theorem and began to develop a mathematical theory that would later become infinitesimal calculus. Soon after Newton had obtained his degree in August of 1665, the University closed down as a precaution against the Great Plague. Although he had been undistinguished as a Cambridge student,^[11] Newton's private studies at his home in Woolsthorpe over the subsequent two years saw the development of his theories on calculus, optics and the law of gravitation.

Middle years

Mathematics

Most modern historians believe that Newton and Leibniz developed infinitesimal calculus independently, using their own unique notations. According to Newton's inner circle, Newton had worked out his method years before Leibniz, yet he published almost nothing about it until 1693, and did not give a full account until 1704. Meanwhile, Leibniz began publishing a full account of his methods in 1684. Moreover, Leibniz's notation and "differential Method" were universally adopted on the Continent, and after 1820 or so, in the British Empire. Whereas Leibniz's notebooks show the advancement of the ideas from early stages until maturity, there is only the end product in Newton's known notes. Newton claimed that he had been reluctant to publish his calculus because he feared being mocked for it. Newton had a very close relationship with Swiss mathematician Nicolas Fatio de Duillier, who from the beginning was impressed by Newton's gravitational theory. In 1691 Duillier planned to prepare a new version of Newton's Philosophiae Naturalis Principia Mathematica, but never finished it. However, in 1694 the relationship between the two men changed. At the time, Duillier had also exchanged several letters with Leibniz^{[citation needed]}.

Starting in 1699, other members of the Royal Society (of which Newton was a member) accused Leibniz of plagiarism, and the dispute broke out in full force in 1711. Newton's Royal Society proclaimed in a study that it was Newton who was the true discoverer and labeled Leibniz a fraud. This study was cast into doubt when it was later found that Newton himself wrote the study's concluding remarks on Leibniz. Thus began the bitter Newton v. Leibniz calculus controversy, which marred the lives of both Newton and Leibniz until the latter's death in 1716.

Newton is generally credited with the generalised binomial theorem, valid for any exponent. He discovered Newton's identities, Newton's method, classified cubic plane curves (polynomials of degree three in two variables), made substantial contributions to the theory of finite differences, and was the first to use fractional indices and to employ coordinate geometry to derive solutions to Diophantine equations. He approximated partial sums of the harmonic series by logarithms (a precursor to Euler's summation formula), and was the first to use power series with confidence and to revert power series. He also discovered a new formula for calculating pi.

He was elected Lucasian Professor of Mathematics in 1669. In that day, any fellow of Cambridge or Oxford had to be an ordained Anglican priest. However, the terms of the Lucasian professorship required that the holder not be active in the church (presumably so as to have more time for science). Newton argued that this should exempt him from the ordination requirement, and Charles II, whose permission was needed, accepted this argument. Thus a conflict between Newton's religious views and Anglican orthodoxy was averted.

Optics

From 1670 to 1672, Newton lectured on optics. During this period he investigated the refraction of light, demonstrating that a prism could decompose white light into a spectrum of colours, and that a lens and a second prism could recompose the multicoloured spectrum into white light.

He also showed that the coloured light does not change its properties by separating out a coloured beam and shining it on various objects. Newton noted that regardless of whether it was reflected or scattered or transmitted, it stayed the same colour. Thus, he observed that colour is the result of objects interacting with already-coloured light rather than objects generating the colour themselves. This is known as Newton's theory of colour.

From this work he concluded that any refracting telescope would suffer from the dispersion of light into colours (chromatic aberration), and invented a type reflecting telescope (today known as a Newtonian telescope) to bypass that problem. By grinding his own mirrors, using Newton's rings to judge the quality of the optics for his telescopes, he was able to produce a superior instrument to the refracting telescope, due primarily to the wider diameter of the mirror. In 1671 the Royal Society asked for a demonstration of his reflecting telescope. Their interest encouraged him to publish his notes On Colour, which he later expanded into his Opticks. When Robert Hooke criticised some of Newton's ideas, Newton was so offended that he withdrew from public debate. The two men remained enemies until Hooke's death.

Newton argued that light is composed of particles or corpuscles, which were refracted by accelerating toward the denser medium, but he had to associate them with waves to explain the diffraction of light (Opticks Bk. II, Props. XII-L). Later physicists instead favoured a purely wavelike explanation of light to account for diffraction. Today's quantum mechanics, photons and the idea of wave–particle duality bear only a minor resemblance to Newton's understanding of light.

In his Hypothesis of Light of 1675, Newton posited the existence of the ether to transmit forces between particles. The contact with the theosophist Henry More, revived his interest in alchemy. He replaced the ether with occult forces based on Hermetic ideas of attraction and repulsion between particles. John Maynard Keynes, who acquired many of Newton's writings on alchemy, stated that "Newton was not the first of the age of reason: he was the last of the magicians."^[12] Newton's interest in alchemy cannot be isolated from his contributions to science.^[13] (This was at a time when there was no clear distinction between alchemy and science.) Had he not relied on the occult idea of action at a distance, across a vacuum, he might not have developed his theory of gravity. (See also Isaac Newton's occult studies.)

In 1704 Newton published Opticks, in which he expounded his corpuscular theory of light. He considered light to be made up of extremely subtle corpuscles, that ordinary matter was made of grosser corpuscles and speculated that through a kind of alchemical transmutation "Are not gross Bodies and Light convertible into one another, …and may not Bodies receive much of their Activity from the Particles of Light which enter their Composition?"^[14] Newton also constructed a primitive form of a frictional electrostatic generator, using a glass globe (Optics, 8th Query).

Mechanics and gravitation

Newton's own copy of his Principia, with hand-written corrections for the second edition

Further information: Writing of Principia Mathematica

In 1677, Newton returned to his work on mechanics, i.e., gravitation and its effect on the orbits of planets, with reference to Kepler's laws of planetary motion, and consulting with Hooke and Flamsteed on the subject. He published his results in De motu corporum in gyrum (1684). This contained the beginnings of the laws of motion that would inform the Principia.

The Philosophiae Naturalis Principia Mathematica (now known as the Principia) was published on 5 July 1687 with encouragement and financial help from Edmond Halley. In this work Newton stated the three universal laws of motion that were not to be improved upon for more than two hundred years. He used the Latin word gravitas (weight) for the effect that would become known as gravity, and defined the law of universal gravitation. In the same work he presented the first analytical determination, based on Boyle's law, of the speed of sound in air. Newton's postulate of an invisible force able to act over vast distances led to him being criticised for introducing "occult agencies" into science.^[15]

With the Principia, Newton became internationally recognised. He acquired a circle of admirers, including the Swiss-born mathematician Nicolas Fatio de Duillier, with whom he formed an intense relationship that lasted until 1693. The end of this friendship led Newton to a nervous breakdown.^{[clarification needed][citation needed]}

Later life

Isaac Newton in old age in 1712, portrait by Sir James Thornhill

Newton's grave in Westminster Abbey

Main article: Isaac Newton's later life

In the 1690s, Newton wrote a number of religious tracts dealing with the literal interpretation of the Bible. Henry More's belief in the Universe and rejection of Cartesian dualism may have influenced Newton's religious ideas. A manuscript he sent to John Locke in which he disputed the existence of the Trinity was never published. Later works – The Chronology of Ancient Kingdoms Amended (1728) and Observations Upon the Prophecies of Daniel and the Apocalypse of St. John (1733) – were published after his death. He also devoted a great deal of time to alchemy (see above).

Newton was also a member of the Parliament of England from 1689 to 1690 and in 1701, but his only recorded comments were to complain about a cold draught in the chamber and request that the window be closed.

Newton moved to London to take up the post of warden of the Royal Mint in 1696, a position that he had obtained through the patronage of Charles Montagu, 1st Earl of Halifax, then Chancellor of the Exchequer. He took charge of England's great recoining, somewhat treading on the toes of Master Lucas (and securing the job of deputy comptroller of the temporary Chester branch for Edmond Halley). Newton became perhaps the best-known Master of the Mint upon Lucas' death in 1699, a position Newton held until his death. These appointments were intended as sinecures, but Newton took them seriously, retiring from his Cambridge duties in 1701, and exercising his power to reform the currency and punish clippers and counterfeiters. As Master of the Mint in 1717 Newton unofficially moved the Pound Sterling from the silver standard to the gold standard by creating a relationship between gold coins and the silver penny in the "Law of Queen Anne"; these were all great reforms at the time, adding considerably to the wealth and stability of England. It was his work at the Mint, rather than his earlier contributions to science, that earned him a knighthood from Queen Anne in 1705.^{[clarification needed]}

Newton was made President of the Royal Society in 1703 and an associate of the French Académie des Sciences. In his position at the Royal Society, Newton made an enemy of John Flamsteed, the Astronomer Royal, by prematurely publishing Flamsteed's star catalogue, which Newton had used in his studies.

Newton died in London on 31 March 1727 [OS: 20 March 1726]^[1], and was buried in Westminster Abbey. His half-niece, Catherine Barton Conduitt,^[16] served as his hostess in social affairs at his house on Jermyn Street in London; he was her "very loving Uncle,"^[17] according to his letter to her when she was recovering from smallpox. Newton, who had no children, had divested much of his estate onto relatives in his last years, and died intestate.

After his death, Newton's body was discovered to have had massive amounts of mercury in it, probably resulting from his alchemical pursuits. Mercury poisoning could explain Newton's eccentricity in late life.^[18]

Religious views

Main article: Isaac Newton's religious views

Historian Stephen D. Snobelen says of Newton, "Isaac Newton was a heretic. But like Nicodemus, the secret disciple of Jesus, he never made a public declaration of his private faith – which the orthodox would have deemed extremely radical. He hid his faith so well that scholars are still unravelling his personal beliefs."^[19] Snobelen concludes that Newton was at least a Socinian sympathiser (he owned and had thoroughly read at least eight Socinian books), possibly an Arian and almost certainly an antitrinitarian.^[19] In an age notable for its religious intolerance there are few public expressions of Newton's radical views, most notably his refusal to take holy orders and his refusal, on his death bed, to take the sacrament when it was offered to him.^[19]

In a view disputed by Snobelen,^[19] T.C. Pfizenmaier argues that Newton held the Eastern Orthodox view of the Trinity rather than the Western one held by Roman Catholics, Anglicans, and most Protestants.^[20] In his own day, he was also accused of being a Rosicrucian (as were many in the Royal Society and in the court of Charles II).^[21]

Although the laws of motion and universal gravitation became Newton's best-known discoveries, he warned against using them to view the Universe as a mere machine, as if akin to a great clock. He said, "Gravity explains the motions of the planets, but it cannot explain who set the planets in motion. God governs all things and knows all that is or can be done."^[22]

His scientific fame notwithstanding, Newton's studies of the Bible and of the early Church Fathers were also noteworthy. Newton wrote works on textual criticism, most notably An Historical Account of Two Notable Corruptions of Scripture. He also placed the crucifixion of Jesus Christ at 3 April, AD 33, which agrees with one traditionally accepted date.^[23] He also attempted, unsuccessfully, to find hidden messages within the Bible.

In his own lifetime, Newton wrote more on religion than he did on natural science. He believed in a rationally immanent world, but he rejected the hylozoism implicit in Leibniz and Baruch Spinoza. Thus, the ordered and dynamically informed Universe could be understood, and must be understood, by an active reason, but this Universe, to be perfect and ordained, had to be regular^{[citation needed]}.

Newton's effect on religious thought

Newton and Robert Boyle’s mechanical philosophy was promoted by rationalist pamphleteers as a viable alternative to the pantheists and enthusiasts, and was accepted hesitantly by orthodox preachers as well as dissident preachers like the latitudinarians.^[24] Thus, the clarity and simplicity of science was seen as a way to combat the emotional and metaphysical superlatives of both superstitious enthusiasm and the threat of atheism,^[25] and, at the same time, the second wave of English deists used Newton's discoveries to demonstrate the possibility of a "Natural Religion."

"Newton," by William Blake; here, Newton is depicted as a "divine geometer"

The attacks made against pre-Enlightenment "magical thinking," and the mystical elements of Christianity, were given their foundation with Boyle’s mechanical conception of the Universe. Newton gave Boyle’s ideas their completion through mathematical proofs and, perhaps more importantly, was very successful in popularising them.^[26] Newton refashioned the world governed by an interventionist God into a world crafted by a God that designs along rational and universal principles.^[27] These principles were available for all people to discover, allowed people to pursue their own aims fruitfully in this life, not the next, and to perfect themselves with their own rational powers.^[28]

Newton saw God as the master creator whose existence could not be denied in the face of the grandeur of all creation.^[29][30][31] But the unforeseen theological consequence of his conception of God, as Leibniz pointed out, was that God was now entirely removed from the world’s affairs, since the need for intervention would only evidence some imperfection in God’s creation, something impossible for a perfect and omnipotent creator.^[32] Leibniz's theodicy cleared God from the responsibility for "l'origine du mal" by making God removed from participation in his creation. The understanding of the world was now brought down to the level of simple human reason, and humans, as Odo Marquard argued, became responsible for the correction and elimination of evil.^[33]

On the other hand, latitudinarian and Newtonian ideas taken too far resulted in the millenarians, a religious faction dedicated to the concept of a mechanical Universe, but finding in it the same enthusiasm and mysticism that the Enlightenment had fought so hard to extinguish.^[34]

Views of the end of the world

See also: Isaac Newton's occult studies

See also: Eschatology

In a manuscript he wrote in 1704 in which he describes his attempts to extract scientific information from the Bible, he estimated that the world would end no earlier than 2060. In predicting this he said, "This I mention not to assert when the time of the end shall be, but to put a stop to the rash conjectures of fanciful men who are frequently predicting the time of the end, and by doing so bring the sacred prophesies into discredit as often as their predictions fail."^[35]

Newton and the counterfeiters

As warden of the Royal Mint, Newton estimated that 20% of the coins taken in during The Great Recoinage were counterfeit. Counterfeiting was high treason, punishable by being hanged, drawn and quartered. Despite this, convictions of the most flagrant criminals could be extremely difficult to achieve; however, Newton proved to be equal to the task.

Disguised as an habitué of bars and taverns, he gathered much of that evidence himself. For all the barriers placed to prosecution, and separating the branches of government, English law still had ancient and formidable customs of authority. Newton was made a justice of the peace and between June 1698 and Christmas 1699 conducted some 200 cross-examinations of witnesses, informers and suspects. Newton won his convictions and in February 1699, he had ten prisoners waiting to be executed.

Possibly Newton's greatest triumph as the king's attorney was against William Chaloner. One of Chaloner's schemes was to set up phony conspiracies of Catholics and then turn in the hapless conspirators whom he entrapped. Chaloner made himself rich enough to posture as a gentleman. Petitioning Parliament, Chaloner accused the Mint of providing tools to counterfeiters (a charge also made by others). He proposed that he be allowed to inspect the Mint's processes in order to improve them. He petitioned Parliament to adopt his plans for a coinage that could not be counterfeited, while at the same time striking false coins. Newton was outraged, and went about the work to uncover anything about Chaloner. During his studies, he found that Chaloner was engaged in counterfeiting. He immediately put Chaloner on trial, but Chaloner had friends in high places and, to Newton's horror, Chaloner walked free. Newton put him on trial a second time with conclusive evidence. Chaloner was convicted of high treason and hanged, drawn and quartered on 23 March 1699 at Tyburn gallows.^[36]

Enlightenment philosophers

Enlightenment philosophers chose a short history of scientific predecessors — Galileo, Boyle, and Newton principally — as the guides and guarantors of their applications of the singular concept of Nature and Natural Law to every physical and social field of the day. In this respect, the lessons of history and the social structures built upon it could be discarded.^[37]

It was Newton’s conception of the Universe based upon Natural and rationally understandable laws that became the seed for Enlightenment ideology. Locke and Voltaire applied concepts of Natural Law to political systems advocating intrinsic rights; the physiocrats and Adam Smith applied Natural conceptions of psychology and self-interest to economic systems and the sociologists criticised the current social order for trying to fit history into Natural models of progress. Monboddo and Samuel Clarke resisted elements of Newton's work, but eventually rationalised it to conform with their strong religious views of nature.

Newton's laws of motion

Classical mechanics

Newton's Second Law

History of ... [show]Fundamental concepts Space · Time · Mass · Force Energy · Momentum [show]Formulations Newtonian mechanics Lagrangian mechanics Hamiltonian mechanics [show]Branches Statics Dynamics Kinematics Applied mechanics Celestial mechanics Continuum mechanics Statistical mechanics [hide]Scientists Newton · Euler · d'Alembert · Clairaut Lagrange · Laplace · Hamilton · Poisson

This box: view • talk • edit

Main article: Newton's laws of motion

The famous three laws of motion:

Newton's First Law (also known as the Law of Inertia) states that an object at rest tends to stay at rest and that an object in uniform motion tends to stay in uniform motion unless acted upon by a net external force.

Newton's Second Law states that an applied force, , on an object equals the rate of change of its momentum, , with time. Mathematically, this is expressed as

Since the second law applies to a system with constant mass, (dm/dt = 0), the first term vanishes, and the equation can be written in the iconic form

where

This equation states that a force applied to an object of mass 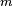causes it to accelerate at a rate .

This equality requires a consistent set of units for measuring mass, length, and time. One such set is the SI system, where mass is in kilograms, length in metres, and time in seconds. This leads to force being in newtons, named in his honour, and acceleration in metres per second per second. The English analogous system is slugs, feet, and seconds.

Newton's Third Law states that for every action there is an equal and opposite reaction. This means that any force exerted onto an object has a counterpart force that is exerted in the opposite direction back onto the first object. The most common example is of two ice skaters pushing against each other and sliding apart in opposite directions. Another example is the recoil of a firearm, in which the force propelling the bullet is exerted equally back onto the gun and is felt by the shooter. Since the objects in question do not necessarily have the same mass, the resulting acceleration of the two objects can be different (as in the case of firearm recoil).

Newton's apple

 

Reputed descendants of Newton's apple tree, at the Botanic Gardens in Cambridge and the Instituto Balseiro library garden

When Newton saw an apple fall, he found
In that slight startle from his contemplation –
'Tis said (for I'll not answer above ground
For any sage's creed or calculation) –
A mode of proving that the earth turn'd round
In a most natural whirl, called "gravitation;"
And this is the sole mortal who could grapple,
Since Adam, with a fall or with an apple.^[38]

Newton himself often told that story that he was inspired to formulate his theory of gravitation by watching the fall of an apple from a tree. It fell straight down — why was that, he asked?

Cartoons have gone further to suggest the apple actually hit Newton's head, and that its impact somehow made him aware of the force of gravity. It is known from his notebooks that Newton was grappling in the late 1660s with the idea that terrestrial gravity extends, in an inverse-square proportion, to the Moon; however it took him two decades to develop the full-fledged theory.^[39] John Conduitt, Newton's assistant at the Royal Mint and husband of Newton's niece, described the event when he wrote about Newton's life:

In the year 1666 he retired again from Cambridge to his mother in Lincolnshire. Whilst he was pensively meandering in a garden it came into his thought that the power of gravity (which brought an apple from a tree to the ground) was not limited to a certain distance from earth, but that this power must extend much further than was usually thought. Why not as high as the Moon said he to himself & if so, that must influence her motion & perhaps retain her in her orbit, whereupon he fell a calculating what would be the effect of that supposition.^[40]

The question was not whether gravity existed, but whether it extended so far from Earth that it could also be the force holding the moon to its orbit. Newton showed that if the force decreased as the inverse square of the distance, one could indeed calculate the Moon's orbital period, and get good agreement. He guessed the same force was responsible for other orbital motions, and hence named it "universal gravitation".

A contemporary writer, William Stukeley, recorded in his Memoirs of Sir Isaac Newton's Life a conversation with Newton in Kensington on 15 April 1726, in which Newton recalled "when formerly, the notion of gravitation came into his mind. It was occasioned by the fall of an apple, as he sat in contemplative mood. Why should that apple always descend perpendicularly to the ground, thought he to himself. Why should it not go sideways or upwards, but constantly to the Earth's centre." In similar terms, Voltaire wrote in his Essay on Epic Poetry (1727), "Sir Isaac Newton walking in his gardens, had the first thought of his system of gravitation, upon seeing an apple falling from a tree." These accounts are probably exaggerations of Newton's own tale about sitting by a window in his home (Woolsthorpe Manor) and watching an apple fall from a tree.

Various trees are claimed to be "the" apple tree which Newton describes. The King's School, Grantham, claims that the tree was purchased by the school, uprooted and transported to the headmaster's garden some years later, the staff of the [now] National Trust-owned Woolsthorpe Manor dispute this, and claim that a tree present in their gardens is the one described by Newton. A descendant of the original tree can be seen growing outside the main gate of Trinity College, Cambridge, below the room Newton lived in when he studied there. The National Fruit Collection at Brogdale^[41] can supply grafts from their tree, which appears identical to Flower of Kent, a coarse-fleshed cooking variety.^[42]

Writings by Newton

• Method of Fluxions (1671)
• Of Natures Obvious Laws & Processes in Vegetation (unpublished, c. 1671–75)^[43]
• De Motu Corporum in Gyrum (1684)
• Philosophiae Naturalis Principia Mathematica (1687)
• Opticks (1704)
• Reports as Master of the Mint (1701–25)
• Arithmetica Universalis (1707)
• The System of the World, Optical Lectures, The Chronology of Ancient Kingdoms, (Amended) and De mundi systemate (published posthumously in 1728)
• Observations on Daniel and The Apocalypse of St. John (1733)
• An Historical Account of Two Notable Corruptions of Scripture (1754)

Fame

French mathematician Joseph-Louis Lagrange often said that Newton was the greatest genius who ever lived, and once added that he was also "the most fortunate, for we cannot find more than once a system of the world to establish."^[44] English poet Alexander Pope was moved by Newton's accomplishments to write the famous epitaph:

Nature and nature's laws lay hid in night;
God said "Let Newton be" and all was light.

Newton himself was rather more modest of his own achievements, famously writing in a letter to Robert Hooke in February 1676

If I have seen further it is by standing on the shoulders of giants

Historians generally think the above quote was an attack on Hooke (who was short and hunchbacked), rather than – or in addition to – a statement of modesty. The two were in a dispute over optical discoveries at the time. The latter interpretation also fits with many of his other disputes over his discoveries – such as the question of who discovered calculus as discussed above.

And then in a memoir later

I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.^[45]

Newton in popular culture

A character based on Isaac Newton plays a significant role in The Age of Unreason, a series of four alternate history novels written by American science fiction and fantasy author Gregory Keyes.

Newton is an important character in The Baroque Cycle by Neal Stephenson. A major theme of these novels is the emergence of modern science, with Newton's work in the Principia being prominent. Newton's interest in alchemy and the dispute over the discovery of calculus are prominent plot points, and there is a (fictional) debate on metaphysics between Newton and Gottfried Leibniz moderated by Caroline of Ansbach. The development of an economy based on money and credit is also a major theme, with Newton's time with the Royal Mint and intrigues against counterfeit leading to a Trial of the Pyx.

In 2007, David Warner portrayed Newton in the Doctor Who audio drama Circular Time.

Monuments and commemoration

Newton statue on display at the Oxford University Museum of Natural History

Newton's monument (1731) can be seen in Westminster Abbey, at the north of the entrance to the choir against the choir screen. It was executed by the sculptor Michael Rysbrack (1694–1770) in white and grey marble with design by the architect William Kent (1685–1748). The monument features a figure of Newton reclining on top of a sarcophagus, his right elbow resting on several of his great books and his left hand pointing to a scroll with a mathematical design. Above him is a pyramid and a celestial globe showing the signs of the Zodiac and the path of the comet of 1680. A relief panel depicts putti using instruments such as a telescope and prism.^[46] The Latin inscription on the base translates as:

Here is buried Isaac Newton, Knight, who by a strength of mind almost divine, and mathematical principles peculiarly his own, explored the course and figures of the planets, the paths of comets, the tides of the sea, the dissimilarities in rays of light, and, what no other scholar has previously imagined, the properties of the colours thus produced. Diligent, sagacious and faithful, in his expositions of nature, antiquity and the holy Scriptures, he vindicated by his philosophy the majesty of God mighty and good, and expressed the simplicity of the Gospel in his manners. Mortals rejoice that there has existed such and so great an ornament of the human race! He was born on 25 December 1642, and died on 20 March 1726/7. — Translation from G.L. Smyth, The Monuments and Genii of St. Paul's Cathedral, and of Westminster Abbey (1826), ii, 703–4.^[46]

A statue of Isaac Newton, standing over an apple, can be seen at the Oxford University Museum of Natural History.

From 1978 until 1988, an image of Newton designed by Harry Ecclestone appeared on Series D £1 banknotes issued by the Bank of England (the last £1 notes to be issued by the Bank of England). Newton was shown on the reverse of the notes holding a book and accompanied by a telescope, a prism and a map of the Solar System.^[47]

See also

Ismaël Bullialdus De Motu (Berkeley's essay) Elements of the Philosophy of Newton Gauss–Newton algorithm History of calculus List of independent discoveries Newton's cannonball Newton disc Newton fractal

Newton's inequalities Newton's laws of motion Newton's notation Newton polygon Newton polynomial Newton's religious views Newton series Newton's theorem of revolving orbits Newton (unit)

Newton–Cotes formulas Newton–Euler equations Newtonianism Schrödinger–Newton equations Scientific Revolution Spalding Gentlemen’s Society "Standing on the shoulders of giants"

Footnotes and references

1. ^ ^{a b c d e} During Newton's lifetime, two calendars were in use in Europe: the Julian or 'Old Style' in Britain and parts of northern Europe (Protestant) and eastern Europe, and the Gregorian or 'New Style', in use in Roman Catholic Europe and elsewhere. At Newton's birth, Gregorian dates were ten days ahead of Julian dates: thus Newton was born on Christmas Day, 25 December 1642 by the Julian calendar, but on 4 January 1643 by the Gregorian. By the time he died, the difference between the calendars had increased to eleven days. Moreover, prior to the adoption of the Gregorian calendar in the UK in 1752, the English new year began (for legal and some other civil purposes) on 25 March ('Lady Day', i.e. the feast of the Annunciation: sometimes called 'Annunciation Style') rather than on 1 January (sometimes called 'Circumcision Style'). Unless otherwise noted, the remainder of the dates in this article follow the Julian Calendar.
2. ^ Dictionary of Scientific Biography, Newton, Isaac, n.4
3. ^ Gjersten, Derek (1986). The Newton Handbook. London: Routledge & Kegan Paul. 
4. ^ "A ranking of the most influential persons in history". eircom.net.
5. ^ Reflecting telescopes Historical Introduction – The Early Period (1608–1672)
6. ^ "Newton beats Einstein in polls of scientists and the public". The Royal Society.
7. ^ Cohen, I.B. (1970). Dictionary of Scientific Biography, Vol. 11, p.43. New York: Charles Scribner's Sons
8. ^ Bell, E.T. (1986) [1937]. Men of Mathematics (Touchstone edition ed.). New York: Simon & Schuster. pp. 91–2. 
9. ^ Book Review Isaac Newton biography December 2003
10. ^ Stillwell, John (2002) [1989]. "Calculus [sub-chapter 9.7 Biographical Notes: Wallis, Newton, and Leibniz]". in S. Axler, F. W. Gehring, K. A. Ribet (editors) (Hardcover). Mathematics and Its History. Undergraduate Texts in Mathematics (2nd edition ed.). New York: Springer-Verlag New York. p. 163. ISBN 0-387-95336-1. "In 1661 he entered Trinity College, Cambridge, as a sizar. Sizars had to earn their keep as servants to wealthier students, and it was indicative of his mother's meanness that he had to become one, for she could afford to support him but chose not to." 
11. ^ ed. Michael Hoskins (1997). Cambridge Illustrated History of Astronomy, p. 159. Cambridge University Press
12. ^ Keynes, John Maynard (1972). "Newton, The Man". The Collected Writings of John Maynard Keynes Volume X. MacMillan St. Martin's Press. pp. 363–4. 
13. ^ Newton apparently abandoned his alchemical researches. See Westfall, Richard S. (1983) [1980]. "Never at Rest: A Biography of Isaac Newton. Cambridge: Cambridge University Press. pp. 530–1. 
14. ^ Dobbs, J.T. (December 1982). "Newton's Alchemy and His Theory of Matter". Isis 73 (4): 511. doi:10.1086/353114.  quoting Opticks
15. ^ Edelglass et al., Matter and Mind, ISBN 0940262452. p. 54
16. ^ Westfall 1980, p. 44.
17. ^ Westfall 1980, p. 595
18. ^ "Newton, Isaac (1642-1727)". Eric Weisstein's World of Biography. Retrieved on 2006-08-30.
19. ^ ^{a b c d} Snobelen, Stephen D. (1999). "Isaac Newton, heretic : the strategies of a Nicodemite" (PDF). British Journal for the History of Science 32: 381–419. doi:10.1017/S0007087499003751. http://www.isaac-newton.org/heretic.pdf. 
20. ^ Pfizenmaier, T.C. (1997). "Was Isaac Newton an Arian?". Journal of the History of Ideas 68 (1): 57–80. 
21. ^ Yates, Frances A. (1972). The Rosicrucian Enlightenment. London: Routledge. 
22. ^ Tiner, J.H. (1975). Isaac Newton: Inventor, Scientist and Teacher. Milford, Michigan, U.S.: Mott Media. 
23. ^ John P. Meier, A Marginal Jew, v. 1, pp. 382–402 after narrowing the years to 30 or 33, provisionally judges 30 most likely.
24. ^ Jacob, Margaret C. (1976). The Newtonians and the English Revolution: 1689–1720. Cornell University Press. pp. 37,44. 
25. ^ Westfall, Richard S. (1958). Science and Religion in Seventeenth-Century England. New Haven: Yale University Press. p. 200. 
26. ^ Haakonssen, Knud. "The Enlightenment, politics and providence: some Scottish and English comparisons". in Martin Fitzpatrick ed.. Enlightenment and Religion: Rational Dissent in eighteenth-century Britain. Cambridge: Cambridge University Press. p. 64. 
27. ^ Frankel, Charles (1948). The Faith of Reason: The Idea of Progress in the French Enlightenment. New York: King's Crown Press. p. 1. 
28. ^ Germain, Gilbert G.. A Discourse on Disenchantment: Reflections on Politics and Technology. p. 28. 
29. ^ Principia, Book III; cited in; Newton’s Philosophy of Nature: Selections from his writings, p. 42, ed. H.S. Thayer, Hafner Library of Classics, NY, 1953.
30. ^ A Short Scheme of the True Religion, manuscript quoted in Memoirs of the Life, Writings and Discoveries of Sir Isaac Newton by Sir David Brewster, Edinburgh, 1850; cited in; ibid, p. 65.
31. ^ Webb, R.K. ed. Knud Haakonssen. “The emergence of Rational Dissent.” Enlightenment and Religion: Rational Dissent in eighteenth-century Britain. Cambridge University Press, Cambridge: 1996. p19.
32. ^ Westfall, Richard S. Science and Religion in Seventeenth-Century England. p201.
33. ^ Marquard, Odo. "Burdened and Disemburdened Man and the Flight into Unindictability," in Farewell to Matters of Principle. Robert M. Wallace trans. London: Oxford UP, 1989.
34. ^ Jacob, Margaret C. The Newtonians and the English Revolution: 1689–1720. p100–101.
35. ^ "Papers Show Isaac Newton's Religious Side, Predict Date of Apocalypse". The Associated Press (19 June 2007). Retrieved on 2007-08-01.
36. ^ Westfall 1980, pp. 571–5
37. ^ Cassels, Alan. Ideology and International Relations in the Modern World. p2.
38. ^ Don Juan (1821), Canto 10, Verse I. In Jerome J. McGann (ed.), Lord Byron: The Complete Poetical Works (1986), Vol. 5, 437
39. ^ I. Bernard Cohen and George E. Smith, eds. The Cambridge Companion to Newton (2002) p. 6
40. ^ Conduitt, John. "Keynes Ms. 130.4:Conduitt's account of Newton's life at Cambridge". Newtonproject. Retrieved on 2006-08-30.
41. ^ "Brogdale - Home of the National Fruit Collection". Brogdale.org.uk. Retrieved on 2008-12-20.
42. ^ "From the National Fruit Collection: Isaac Newton's Tree". Retrieved on 2009-01-10.
43. ^ Newton's alchemical works transcribed and online at Indiana University retrieved 11 January 2007
44. ^ Fred L. Wilson, History of Science: Newton citing: Delambre, M. "Notice sur la vie et les ouvrages de M. le comte J. L. Lagrange," Oeuvres de Lagrange I. Paris, 1867, p. xx.
45. ^ Memoirs of the Life, Writings, and Discoveries of Sir Isaac Newton (1855) by Sir David Brewster (Volume II. Ch. 27)
46. ^ ^{a b} "Monuments & Gravestones: Sir Isaac Newton". Westminster Abbey. Retrieved on 2008-10-20.
47. ^ "Withdrawn banknotes reference guide". Bank of England. Retrieved on 2008-10-17.

Resources

References

• Bell, E.T. (1937). Men of Mathematics. New York: Simon and Schuster. ISBN 0-671-46400-0.  Excerpt
• Christianson, Gale (1984). In the Presence of the Creator: Isaac Newton & His Times. New York: Free Press. ISBN 0-02-905190-8.  This well documented work provides, in particular, valuable information regarding Newton's knowledge of Patristics
• Craig, John (1958). "Isaac Newton – Crime Investigator". Nature 182: 149. doi:10.1038/182149a0. 
• Craig, John (1963). "Isaac Newton and the Counterfeiters". Notes and Records of the Royal Society of London 18: 136. doi:10.1098/rsnr.1963.0017. 
• Westfall, Richard S. (1980, 1998). Never at Rest. Cambridge University Press. ISBN 0-521-27435-4. 
• "Sir Isaac Newton". School of Mathematics and Statistics, University of St. Andrews, Scotland. Retrieved on 8 March 2005.
• "The Newton Project". Imperial College London. Retrieved on 8 March 2005.

Further reading

• Andrade, E. N. De C. (1950). Isaac Newton. New York: Chanticleer Press. 
• Bardi, Jason Socrates. The Calculus Wars: Newton, Leibniz, and the Greatest Mathematical Clash of All Time. (2006). 277 pp. excerpt and text search
• Bechler, Zev (1991). Newton's Physics and the Conceptual Structure of the Scientific Revolution. Springer. ISBN 0792310543. .
• Berlinski, David. Newton's Gift: How Sir Isaac Newton Unlocked the System of the World. (2000). 256 pp. excerpt and text search ISBN 0-684-84392-7
• Buchwald, Jed Z. and Cohen, I. Bernard, eds. Isaac Newton's Natural Philosophy. MIT Press, 2001. 354 pp. excerpt and text search
• Casini, P. (1988). "Newton's Principia and the Philosophers of the Enlightenment". Notes and Records of the Royal Society of London 42 (1): 35–52. doi:10.1098/rsnr.1988.0006. ISSN 0035–9149. http://links.jstor.org/sici?sici=0035-9149%28198801%2942%3A1%3C35%3AN%27ATPO%3E2.0.CO%3B2-H. 
• Christianson, Gale E. (1996). Isaac Newton and the Scientific Revolution. Oxford U. Press. ISBN 019530070X.  See this site for excerpt and text search.
• Christianson, Gale (1984). In the Presence of the Creator: Isaac Newton & His Times. New York: Free Press. ISBN 0-02-905190-8. 
• Cohen, I. Bernard and Smith, George E., ed. The Cambridge Companion to Newton. (2002). 500 pp. focuses on philosophical issues only; excerpt and text search; complete edition online
• Cohen, I. B. (1980). The Newtonian Revolution. Cambridge: Cambridge University Press. 
• Craig, John (1946). Newton at the Mint. Cambridge, England: Cambridge University Press. 
• Dampier, William C.; Dampier, M. (1959). Readings in the Literature of Science. New York: Harper & Row. 
• de Villamil, Richard (1931). Newton, the Man. London: G.D. Knox.  – Preface by Albert Einstein. Reprinted by Johnson Reprint Corporation, New York (1972).
• Dobbs, B. J. T. (1975). The Foundations of Newton's Alchemy or "The Hunting of the Greene Lyon". Cambridge: Cambridge University Press. 
• Gjertsen, Derek (1986). The Newton Handbook. London: Routledge & Kegan Paul. ISBN 0-7102-0279-2. 
• Gleick, James (2003). Isaac Newton. Alfred A. Knopf. ISBN 0375422331. 
• Halley, E. (1687). "Review of Newton's Principia". Philosophical Transactions 186: 291 – 297. 
• Hart, Michael H. (1992). The 100''. Carol Publishing Group. ISBN 0-8065-1350-0.  – paperback
• Hawking, Stephen, ed. On the Shoulders of Giants. ISBN 0-7624-1348-4 Places selections from Newton's Principia in the context of selected writings by Copernicus, Kepler, Galileo and Einstein
• Herivel, J. W. (1965). The Background to Newton's Principia. A Study of Newton's Dynamical Researches in the Years 1664–84. Oxford: Clarendon Press. 
• Keynes, John Maynard (1963). Essays in Biography. W. W. Norton & Co. ISBN 0-393-00189-X.  Keynes took a close interest in Newton and owned many of Newton's private papers.
• Koyré, A. (1965). Newtonian Studies. Chicago: University of Chicago Press. 
• Newton, Isaac. Papers and Letters in Natural Philosophy, edited by I. Bernard Cohen. Harvard University Press, 1958,1978. ISBN 0-674-46853-8.
• Newton, Isaac (1642–1727). The Principia: a new Translation, Guide by I. Bernard Cohen ISBN 0-520-08817-4 University of California (1999)
• Pemberton, H. (1728). A View of Sir Isaac Newton's Philosophy. London: S. Palmer. 
• Shamos, Morris H. (1959). Great Experiments in Physics. New York: Henry Holt and Company, Inc.. 
• Shapley, Harlow, S. Rapport, and H. Wright. A Treasury of Science; "Newtonia" pp. 147–9; "Discoveries" pp. 150–4. Harper & Bros., New York, (1946).
• Simmons, J. (1996). The Giant Book of Scientists  – The 100 Greatest Minds of all Time. Sydney: The Book Company. 
• Stukeley, W. (1936), Memoirs of Sir Isaac Newton's Life, London: Taylor and Francis  (edited by A. H. White; originally published in 1752)
• Westfall, R. S. (1971). Force in Newton's Physics: The Science of Dynamics in the Seventeenth Century. London: Macdonald. 

Newton and religion

• Dobbs, Betty Jo Tetter. The Janus Faces of Genius: The Role of Alchemy in Newton's Thought. (1991), links the alchemy to Arianism
• Force, James E., and Richard H. Popkin, eds. Newton and Religion: Context, Nature, and Influence. (1999), 342pp . Pp. xvii + 325. 13 papers by scholars using newly opened manuscripts
• Ramati, Ayval. "The Hidden Truth of Creation: Newton's Method of Fluxions" British Journal for the History of Science 34: 417–438. in JSTOR, argues that his calculus had a theological basis
• Snobelen, Stephen D. "'God of Gods, and Lord of Lords': The Theology of Isaac Newton's General Scholium to the Principia," Osiris, 2nd Series, Vol. 16, (2001), pp. 169–208 in JSTOR
• Snobelen, Stephen D. "Isaac Newton, Heretic: The Strategies of a Nicodemite," British Journal for the History of Science 32: 381–419. in JSTOR
• Pfizenmaier, Thomas C. "Was Isaac Newton an Arian?," Journal of the History of Ideas, Vol. 58, No. 1 (Jan., 1997), pp. 57–80 in JSTOR
• Westfall, Richard S. Never at Rest: A Biography of Isaac Newton. 2 vol. Cambridge U. Press, 1981. 895 pp. the major scholarly biography excerpt and text search
• Wiles, Maurice. Archetypal Heresy. Arianism through the Centuries. (1996) 214pp, with chapter 4 on 18th century England; pp 77–93 on Newtorn excerpt and text search,

Primary sources

• Newton, Isaac. The Principia: Mathematical Principles of Natural Philosophy. U. of California Press, (1999). 974 pp.
  • Brackenridge, J. Bruce. The Key to Newton's Dynamics: The Kepler Problem and the Principia: Containing an English Translation of Sections 1, 2, and 3 of Book One from the First (1687) Edition of Newton's Mathematical Principles of Natural Philosophy. U. of California Press, 1996. 299 pp.
• Newton, Isaac. The Optical Papers of Isaac Newton. Vol. 1: The Optical Lectures, 1670–1672. Cambridge U. Press, 1984. 627 pp.
  • Newton, Isaac. Opticks (4th ed. 1730) online edition
  • Newton, I. (1952). Opticks, or A Treatise of the Reflections, Refractions, Inflections & Colours of Light. New York: Dover Publications.
• Newton, I. Sir Isaac Newton's Mathematical Principles of Natural Philosophy and His System of the World, tr. A. Motte, rev. Florian Cajori. Berkeley: University of California Press. (1934).
• Whiteside, D. T. (1967–82). The Mathematical Papers of Isaac Newton. Cambridge: Cambridge University Press.  – 8 volumes
• Newton, Isaac. The correspondence of Isaac Newton, ed. H. W. Turnbull and others, 7 vols. (1959–77).
• Newton's Philosophy of Nature: Selections from His Writings edited by H. S. Thayer, (1953), online edition
• Isaac Newton, Sir; J Edleston; Roger Cotes, Correspondence of Sir Isaac Newton and Professor Cotes, including letters of other eminent men, London, John W. Parker, West Strand; Cambridge, John Deighton, 1850. – Google Books
• Maclaurin, C. (1748). An Account of Sir Isaac Newton's Philosophical Discoveries, in Four Books. London: A. Millar and J. Nourse.
• Newton, I. (1958). Isaac Newton's Papers and Letters on Natural Philosophy and Related Documents, eds. I. B. Cohen and R. E. Schofield. Cambridge: Harvard University Press.
• Newton, I. (1962). The Unpublished Scientific Papers of Isaac Newton: A Selection from the Portsmouth Collection in the University Library, Cambridge, ed. A. R. Hall and M. B. Hall. Cambridge: Cambridge University Press.
• Newton, I. (1975). Isaac Newton's 'Theory of the Moon's Motion' (1702). London: Dawson.

  English physicist and mathematician who was born into a poor farming family. Luckily for humanity, Newton was not a good farmer, and was sent to Cambridge to study to become a preacher. At Cambridge, Newton studied mathematics, being especially strongly influenced by Euclid, although he was also influenced by Baconian and Cartesian philosophies. Newton was forced to leave Cambridge when it was closed because of the plague, and it was during this period that he made some of his most significant discoveries. With the reticence he was to show later in life, Newton did not, however, publish his results.

  Newton suffered a mental breakdown in 1675 and was still recovering through 1679. In response to a letter from Hooke, he suggested that a particle, if released, would spiral in to the center of the Earth. Hooke wrote back, claiming that the path would not be a spiral, but an ellipse. Newton, who hated being bested, then proceeded to work out the mathematics of orbits. Again, he did not publish his calculations. Newton then began devoting his efforts to theological speculation and put the calculations on elliptical motion aside, telling Halley he had lost them (Westfall 1993, p. 403). Halley, who had become interested in orbits, finally convinced Newton to expand and publish his calculations. Newton devoted the period from August 1684 to spring 1686 to this task, and the result became one of the most important and influential works on physics of all times, Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy) (1687), often shortened to Principia Mathematica or simply "the Principia."

  In Book I of Principia, Newton opened with definitions and the three laws of motion now known as Newton's laws (laws of inertia, action and reaction, and acceleration proportional to force). Book II presented Newton's new scientific philosophy which came to replace Cartesianism. Finally, Book III consisted of applications of his dynamics, including an explanation for tides and a theory of lunar motion. To test his hypothesis of universal gravitation, Newton wrote Flamsteed to ask if Saturn had been observed to slow down upon passing Jupiter. The surprised Flamsteed replied that an effect had indeed been observed, and it was closely predicted by the calculations Newton had provided. Newton's equations were further confirmed by observing the shape of the Earth to be oblate spheroidal, as Newton claimed it should be, rather than prolate spheroidal, as claimed by the Cartesians. Newton's equations also described the motion of Moon by successive approximations, and correctly predicted the return of Halley's Comet. Newton also correctly formulated and solved the first ever problem in the calculus of variations which involved finding the surface of revolution which would give minimum resistance to flow (assuming a specific drag law).

  Newton invented a scientific method which was truly universal in its scope. Newton presented his methodology as a set of four rules for scientific reasoning. These rules were stated in the Principia and proposed that (1) we are to admit no more causes of natural things such as are both true and sufficient to explain their appearances, (2) the same natural effects must be assigned to the same causes, (3) qualities of bodies are to be esteemed as universal, and (4) propositions deduced from observation of phenomena should be viewed as accurate until other phenomena contradict them.

  These four concise and universal rules for investigation were truly revolutionary. By their application, Newton formulated the universal laws of nature with which he was able to unravel virtually all the unsolved problems of his day. Newton went much further than outlining his rules for reasoning, however, actually describing how they might be applied to the solution of a given problem. The analytic method he invented far exceeded the more philosophical and less scientifically rigorous approaches of Aristotle and Aquinas. Newton refined Galileo's experimental method, creating the compositional method of experimentation still practiced today. In fact, the following description of the experimental method from Newton's Optics could easily be mistaken for a modern statement of current methods of investigation, if not for Newton's use of the words "natural philosophy" in place of the modern term "the physical sciences." Newton wrote, "As in mathematics, so in natural philosophy the investigation of difficult things by the method of analysis ought ever to precede the method of composition. This analysis consists of making experiments and observations, and in drawing general conclusions from them by induction...by this way of analysis we may proceed from compounds to ingredients, and from motions to the forces producing them; and in general from effects to their causes, and from particular causes to more general ones till the argument end in the most general. This is the method of analysis: and the synthesis consists in assuming the causes discovered and established as principles, and by them explaining the phenomena preceding from them, and proving the explanations."

  Newton formulated the classical theories of mechanics and optics and invented calculus years before Leibniz. However, he did not publish his work on calculus until afterward Leibniz had published his. This led to a bitter priority dispute between English and continental mathematicians which persisted for decades, to the detriment of all concerned. Newton discovered that the binomial theorem was valid for fractional powers, but left it for Wallis to publish (which he did, with appropriate credit to Newton). Newton formulated a theory of sound, but derived a speed which did not agree with his experiments. The reason for the discrepancy was that the concept of adiabatic propagation did not yet exist, so Newton's answer was too low by a factor of , where is the ratio of heat capacities of air. Newton therefore fudged his theory until agreement was achieved (Engineering and Science, pp. 15-16).

  In Optics (1704), whose publication Newton delayed until Hooke's death, Newton observed that white light could be separated by a prism into a spectrum of different colors, each characterized by a unique refractivity, and proposed the corpuscular theory of light. Newton's views on optics were born out of the original prism experiments he performed at Cambridge. In his "experimentum crucis" (crucial experiment), he found that the image produced by a prism was oval-shaped and not circular, as current theories of light would require. He observed a half-red, half-blue string through a prism, and found the ends to be disjointed. He also observed Newton's rings, which are actually a manifestation of the wave nature of light which Newton did not believe in. Newton believed that light must move faster in a medium when it is refracted towards the normal, in opposition to the result predicted by Huygens's wave theory.

  Newton also formulated a system of chemistry in Query 31 at the end of Optics. In this corpuscular theory, "elements" consisted of different arrangements of atoms, and atoms consisted of small, hard, billiard ball-like particles. He explained chemical reactions in terms of the chemical affinities of the participating substances. Newton devoted a majority of his free time later in life (after 1678) to fruitless alchemical experiments.

  Newton was extremely sensitive to criticism, and even ceased publishing until the death of his arch-rival Hooke. It was only through the prodding of Halley that Newton was persuaded at all to publish the Principia Mathematica. In the latter portion of his life, he devoted much of his time to alchemical researches and trying to date events in the Bible. After Newton's death, his burial place was moved. During the exhumation, it was discovered that Newton had massive amounts of mercury in his body, probably resulting from his alchemical pursuits. This would certainly explain Newton's eccentricity in late life. Newton was appointed Warden of the British Mint in 1695. Newton was knighted by Queen Anne. However, the act was "an honor bestowed not for his contributions to science, nor for his service at the Mint, but for the greater glory of party politics in the election of 1705" (Westfall 1993, p. 625).

  Newton singlehandedly contributed more to the development of science than any other individual in history. He surpassed all the gains brought about by the great scientific minds of antiquity, producing a scheme of the universe which was more consistent, elegant, and intuitive than any proposed before. Newton stated explicit principles of scientific methods which applied universally to all branches of science. This was in sharp contradistinction to the earlier methodologies of Aristotle and Aquinas, which had outlined separate methods for different disciplines.

  Although his methodology was strictly logical, Newton still believed deeply in the necessity of a God. His theological views are characterized by his belief that the beauty and regularity of the natural world could only "proceed from the counsel and dominion of an intelligent and powerful Being." He felt that "the Supreme God exists necessarily, and by the same necessity he exists always and everywhere." Newton believed that God periodically intervened to keep the universe going on track. He therefore denied the importance of Leibniz's vis viva as nothing more than an interesting quantity which remained constant in elastic collisions and therefore had no physical importance or meaning.

  Although earlier philosophers such as Galileo and John Philoponus had used experimental procedures, Newton was the first to explicitly define and systematize their use. His methodology produced a neat balance between theoretical and experimental inquiry and between the mathematical and mechanical approaches. Newton mathematized all of the physical sciences, reducing their study to a rigorous, universal, and rational procedure which marked the ushering in of the Age of Reason. Thus, the basic principles of investigation set down by Newton have persisted virtually without alteration until modern times. In the years since Newton's death, they have borne fruit far exceeding anything even Newton could have imagined. They form the foundation on which the technological civilization of today rests. The principles expounded by Newton were even applied to the social sciences, influencing the economic theories of Adam Smith and the decision to make the United States legislature bicameral. These latter applications, however, pale in contrast to Newton's scientific contributions.

  It is therefore no exaggeration to identify Newton as the single most important contributor to the development of modern science. The Latin inscription on Newton's tomb, despite its bombastic language, is thus fully justified in proclaiming, "Mortals! rejoice at so great an ornament to the human race!" Alexander Pope's couplet is also apropos: "Nature and Nature's laws lay hid in night; God said, Let Newton be! and all was light."

  Several interesting Newton quotes are given by Misner et al. (1973, pp. 40-41).